La sequenza di Fibonacci la possiamo ritrovare ovunque in natura e, dal punto di vista delle piante, è il modo che esse hanno di crescere organizzandosi nella maniera più efficiente

Non ho mai amato la matematica. Cinque interminabili anni di Liceo scientifico e gli esami di chimica e matematica all’università non mi hanno fatto cambiare idea, ma… in questi giorni mi sono resa conto dell’importanza dei numeri e dell’inviolabilità delle leggi della fisica. Per questo ho deciso di condividere con voi un video bellissimo e qualche informazione che poterebbe avvicinare a questa “conoscenza” chi, come me, non è particolarmente portato. È una delle cose che amavo insegnare ai miei studenti e che riesce a collegare in modo immediato e visibile la matematica alla biologia, all’arte, alla bellezza: la Successione di Fibonacci.

La sequenza di Fibonacci la possiamo ritrovare ovunque in natura e, dal punto di vista delle piante, è il modo che esse hanno di crescere organizzandosi nella maniera più efficiente: in questo modo in una pigna sta un numero maggiore di semi possibile e grazie allo stesso principio le foglie delle piante crescono in modo da ottenere la maggior quantità di luce ciascuna. Se parliamo, invece, di piante grasse o a foglie stratificate (come i cavoli ad esempio), questi numeri permettono un’organizzazione ottimale dello spazio
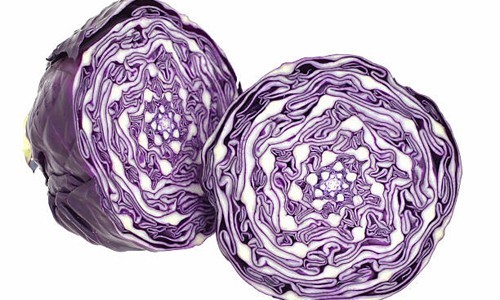
Questi numeri sono applicabili alla crescita di ogni tipo di essere vivente e di ogni sua parte, a partire dalla moltiplicazione cellulare.

I primi due termini della successione sono 1 ed 1. Tutti gli altri termini sono la somma dei due termini che li precedono:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 …
F1 = 1
F2 = 1
F3 = 1 + 1 = 2
F4 = 2 + 1 = 3
F5 = 3 + 2 = 5
F6 = 5 + 3 = 8
F7 = 8 + 5 = 13
F8 = 13 + 8 = 21
F9 = 21 + 13 = 34
…

Una proprietà notevolissima di questi numeri è che il rapporto tra un numero di Fibonacci e quello immediatamente precedente si avvicina sempre di più al numero 1.61803398874989… Questo numero è la famosa Sezione Aurea (o Numero Aureo).
La prossima volta che farete un giro in giardino, o osserverete le spirali del guscio di una conchiglia, ricordatevi che state osservando anche formule matematiche. Ora vi lascio a questo fantastico video, che vale più di mille parole. Alzate il volume, la musica lo rende perfetto. Buona visione!


